logo

Estimating constrained precision matrices with TensorFlow

Gaussian graphical models are defined by the structure of the precision matrix. From a fixed structure, how we estimate the values of the precision matrix? I will show you two slightly different problems using TensorFlow.

Those columns kind of look like a matrix, don’t they? Sort of? Not really. Pretty cool anyways. Image credit: author (Oliver K. Ernst). All rights reserved.

You can see the GitHub repo for this project here. The corresponding package can also be installed with

pip install tfConstrainedGauss

A detailed write up can also be found in the PDF in the [latex](https://github.com/smrfeld/tf-constrained-gauss/blob/main/latex/constrained_gauss.pdf) folder for this repo.

The problem we’re trying to solve

In a Gaussian graphical model, nodes denote random variables, and edges denote interactions. Which edges exist defines the structure of the precision matrix. For example, for the graphical model:

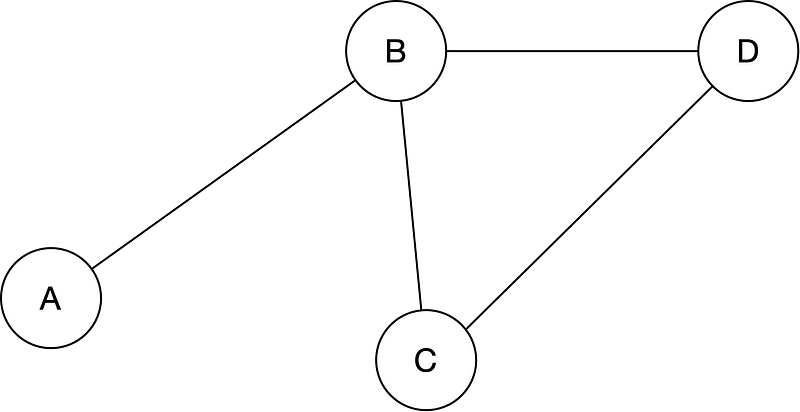
Gaussian graphical model. Note that self-interactions (e.g. lines from A to A) are not shown as typical.

the structure of the precision matrix is:

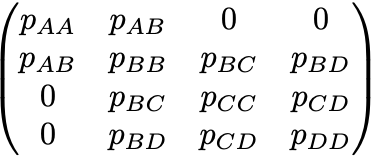
From a given pile of data, we get a covariance matrix from which we would like to estimate the precision matrix. In some applications the goal is to also find the structure of the precision matrix — this is typically done with some form of lasso regularization to knock out small elements. In this article & corresponding Python package, we only consider the case where the structure of the precision matrix is known and fixed (but not its values).

The problem to estimate the precision matrix in this case is one of mixed constraints:

  • Constraints on the precision matrix are those which set some elements to zero.
  • Constraints on the covariance matrix are those given by the data.

This then cannot be solved just by taking a matrix inverse — the problem is best solved by optimization.

Two methods are presented and implemented in the Python package, which are actually solving two slightly different problems:

  1. A maximum entropy (MaxEnt) method. Gaussian distributions are MaxEnt distributions: the constraints are some specified covariances between random variables, and the Lagrange multipliers are the elements of the precision matrix (the edges in the graphical model). Therefore, in this problem setup, the constraints given in the covariance matrix are only those elements corresponding to the non-zero elements of the precision matrix.
  2. A method which minimizes the product of precision and covariance matrix, which should give the identity matrix. In this problem setup, the full covariance matrix is specified as a constraint. Because of this, the problem is over-constrained, and while we may find a “good” solution in the sense that the product of precision and covariance matrices is close to the identity, the elements of the covariance matrix found may not be close to the specified constraints.

Let’s dive deeper into each.

MaxEnt-based method

Given the structure of the n x n precision matrix (i.e. given the Gaussian graphical model), for example:

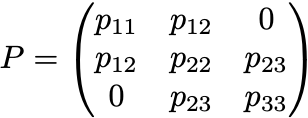
(note that the diagonal elements are always non-zero), and given the covariances for corresponding to every non-zero entry in P, i.e. in this example given the values:

the goal is to find the elements of P. In other words, every unique element (i,j) of the n x n symmetric matrix has a given constraint, either to a value in the covariance matrix, or a zero entry in the precision matrix.

Left: the structure of an example 8x8 precision matrix. Black indicates non-zero elements; white are zero. Right: constraints on the covariance matrix — one constraint is given for every non-zero value in the precision matrix. The other values are not specified.

This is a maximum entropy (MaxEnt) setup. The elements of the precision matrix pij are directly the interactions in the Gaussian graphical model; the moments they control in a MaxEnt sense are the covariances cij.

The problem can be solved in a number of ways, for example using Boltzmann machine learning, where we minimize:

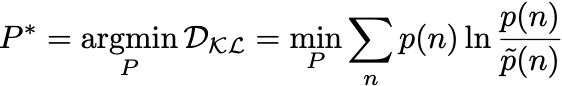
where p(n) is the (unknown) data distribution that gave rise to the given covariances cij and q(n) is the Gaussian with precision matrix P. The gradients that result are the wake sleep phase:

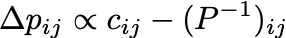
In TensorFlow, we minimize the MSE loss for the individual terms, which results in the same first order gradients:

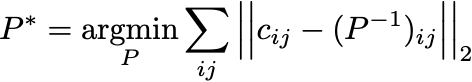
This minimization problem is implemented in the tfConstrainedGauss Python package. It uses Tensorflow to perform the minimization — see also the docs page.

For the precision matrix structure and covariance matrix introduced previously, the result of solving the optimization problem is:

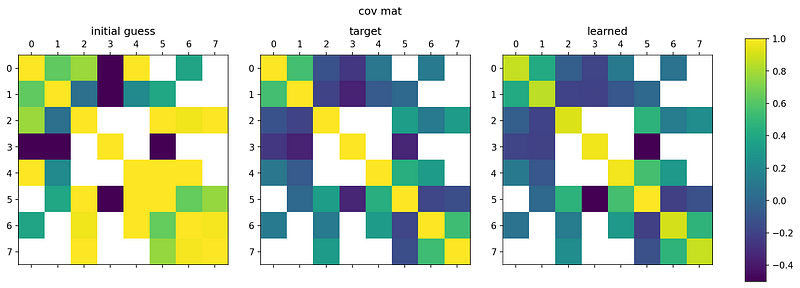
Solving the example problem. Left: the initial guess for the covariance matrix (the elements which are given by the constraints). Middle: the target constraints from before. Right: the final learned covariance matrix after minimizing the L2 loss.

As we can see, the final learned covariance matrix closely matches the constraints.

What is actually learned are the (non-zero) elements of the precision matrix:

Left: The learned precision matrix. Here, white indicates elements which are fixed to be zero. Right: The full learned covariance matrix, i.e. the inverse of the matrix on the left. The elements which were not given by the constraints (those which were left free) are determined by the structure of the precision matrix.

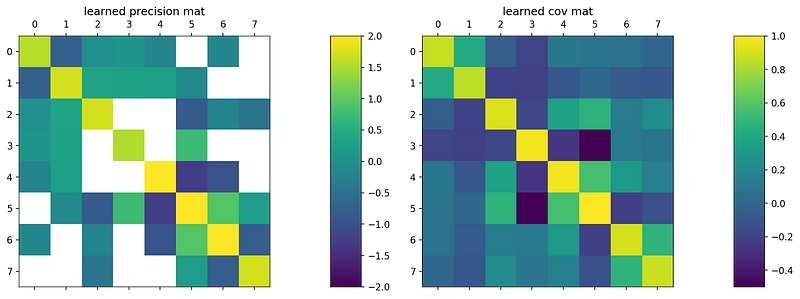
The full covariance matrix on the right (the inverse of the precision matrix on the left) matches the constraints that are given, and fills in the remaining elements based on the specified graphical model.

Note that we can modify the learning algorithm slightly to learn each element of the covariance matrix with equal importance — we can use a weighted MSE loss:

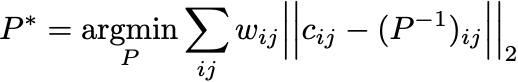
where

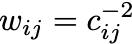
A detailed write up can also be found in the PDF in the [latex](https://github.com/smrfeld/tf-constrained-gauss/blob/main/latex/constrained_gauss.pdf) folder for this repo.

Alternative: identity-based method

Given an n x n covariance matrix, here of size n=3:

and given the structure of the precision matrix (i.e. given the Gaussian graphical model), for example:

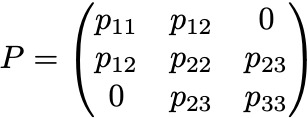
(note that the diagonal elements are always non-zero).

Left: precision matrix structure — black indicates unknown non-zero elements, white indicates fixed zero elements. Right: constraints on covariance matrix.

The goal is to find the elements of the precision matrix by:

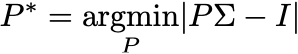
where I is the identity.

Again, this is implemented in Tensorflow in the tfConstrainedGauss package.

The advantage of this approach is that it does not require calculating the inverse of any matrix, particularly important for large n.

The disadvantage of this approach is that the solution found for P may not yield a covariance matrix P^{-1} whose individual elements are close to those of C. That is, while P.C may be close to the identity, there are likely errors in every single element of P^{-1}.

This can be seen in the example from before:

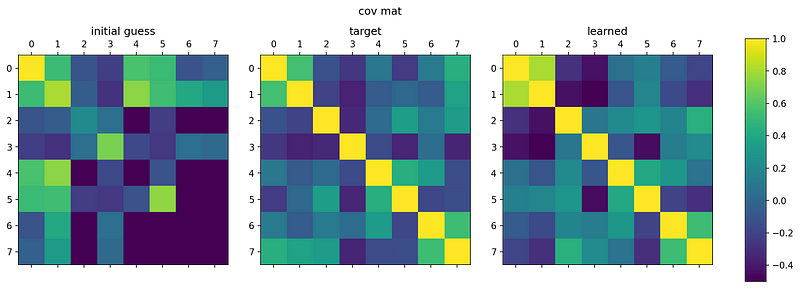
Left: initial guess for the covariance matrix. Middle: true target cov matrix. Right: learned covariance matrix.

Here the final learned covariance matrix on the right (the inverse of the learned precision matrix) actually does not really match the target covariance matrix (middle). The product of the learned precision matrix and given target covariance matrix may be close to the identity, but the inverse of that learned precision matrix — the learned covariance matrix — is off.

Incidentally, the learned precision matrix is:

Learned precision matrix.

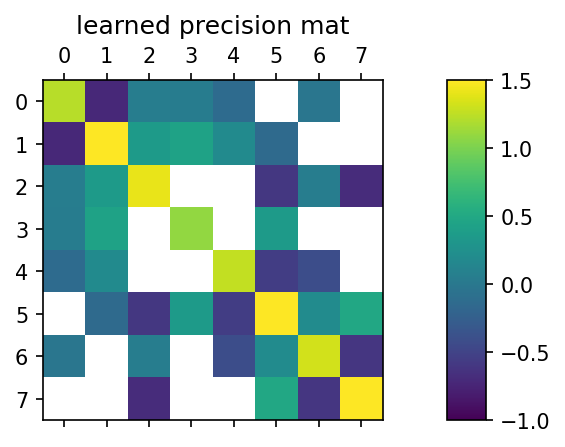
Final thoughts

pip install tfConstrainedGauss

Contents

Oliver K. Ernst
October 2, 2021

Read this on Medium